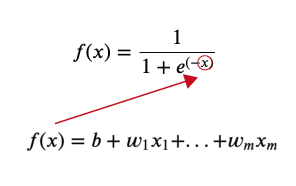【Python】ロジスティック回帰のわかりやすい解説

Itoi Yoshihiko

横浜国立大学理工学部建築都市環境系学科卒
一級鉄筋技能士

線形回帰が理解できたら、次はロジスティック回帰について見ていきます。

ロジスティック回帰は分類モデルに使用され、良い/悪いなどの0/1判定をする機械学習で良く使用されます。

例えば、癌の判定や、迷惑メールの判定などがよく例で出てきます。

線形回帰にシグモイド関数というものが新しく入るので、先に線形回帰を理解しておくことをお勧めします。

難しい数学の知識はできるだけ省いてできるだけ簡単に説明します。

ただ、中盤以降はpythonの基礎的な知識は必要です。

ロジスティック回帰

0か1に分ける方法を二項分類と言います。

機械学習で0か1を判定させるにはどのようなモデルが必要でしょうか？

ここではまずシグモイド関数について詳しく見ていきましょう。

シグモイド関数はS字型

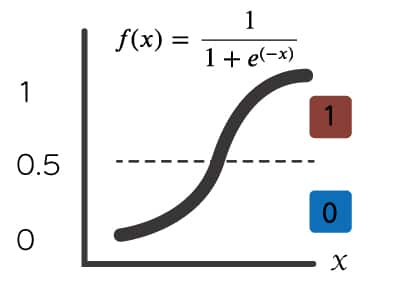
ロジスティック回帰では、下記のようにxを与えると、0〜1の間で変化するシグモイド関数というのがあるので、それを使っていきます。

シグモイド関数からできた値が0.5以上であれば、「１」それ以外なら「０」ということで0/1判定ができます。

$$ f(x) = \frac{1}{1+e^{(-x)}} $$

公式は覚えなくても、こういうS字型になる式というくらいで良いです。

シグモイド関数で得られる値を確率として捉えることができます。

例えば、シグモイド関数から0.7という結果が得られたら、70%で癌であるといった判定がすることができます。

ですので、0.5以上が1ではなく、より厳しく0.8以上なら1ということもできます。

pythonでのコードは下記のようなシンプルなものです。

import math
def sigmoid(x):
    return 1 / (1 + math.e**-x)

import math

def sigmoid(x):

return 1 / (1 + math.e**-x)

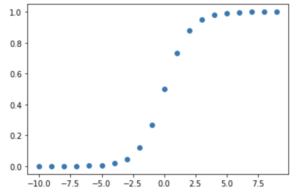
-10〜10でプロットしてみましょう。

import matplotlib.pyplot as plt
x = range(-10,10)
y = [sigmoid(d) for d in x]
plt.scatter(x, y)

import matplotlib.pyplot as plt

x = range(-10,10)

y = [sigmoid(d) for d in x]

plt.scatter(x, y)

期待通りのプロットです。

x と yのデータを作るところは下記コードでも同じですので、分かりやすい方を使ってください。

yには空のリストを用意し、appendメソッドでリストを追加していきます。

x = range(-10,10)
y = []
for d in x:
    y.append(sigmoid(d))

x = range(-10,10)

y = []

for d in x:

y.append(sigmoid(d))

参考のために、シグモイド関数の実装を紹介しましたが、自ら実装することはほぼないので、簡単なんだということがわかっていただければ良いです。

Pythonの配列　listの使い方まとめ

線形回帰とシグモイド関数を組み合わせて0/1の判定モデルを作る

では、線形回帰にどのようにシグモイド関数を組み合わせると0/1の判定ができるのでしょうか？

まず、特徴量xがm個ある線形回帰の式です。

$$ f(x) = b + w_1x_1 + … + w_mx_m $$

次に、先ほど出たシグモイド関数の式です。

$$ f(x) = \frac{1}{1+e^{(-x)}} $$

このシグモイドのxの部分に線形回帰の式を放り込みます。

$$ h(x) = \frac{1}{1+e^{(-b + w_1x_1 + … + w_mx_m)}} $$

この式が、ロジスティック回帰のモデルになります。この式で求めらる結果を$h(x)$とします。

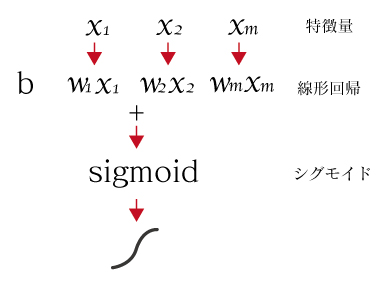
処理イメージは下記のように特徴量＞線形回帰＞シグモイド関数で処理されます。

線型回帰の処理の後にシグモイド関数が引っ付いただけなのが分かりますね。

この処理がされることによって、入力された特徴量は、0〜1の間の値で出力され、0.5以上なら癌であるといった判定などができるようになります。

この処理の流れは、ニューラルネットワークやディープラーニングでも使っています。

シグモイド関数のことを活性化関数ともよびます。

ロジスティック回帰のloss(損失関数)

ロジスティック回帰でも、wとbを機械が決定するために勾配降下法を使います。

勾配降下法ではlossが必要で、線形回帰ではloss = 平均二乗誤差を使いますが、ロジスティック回帰のlossの式はまた別のものを使います。

損失関数にはlogが出てきて、以下のようになります。

$$ loss=-ylog(h(x))-(1-y)log(1-h(x)) $$

ちなみにこの式は覚える必要ないので、こういったlossの式を使っているんだとみておいてください。

教師データの答えであるyは必ず「1」若しくは「0」をとなるので、上記の式は下記のいずれかになります。

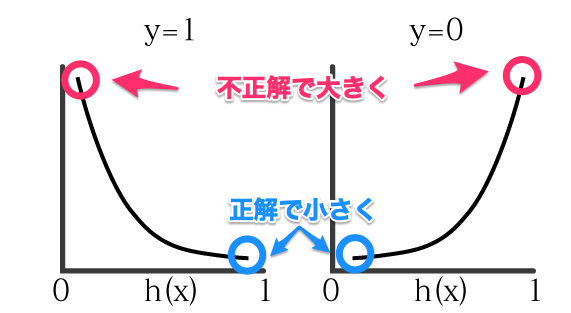
y = 1 : $-log(h(x))$

y = 0 : $-log(1-h(x))$

回帰モデル/(h(x)/)から出てくる値は必ず、0-1の値になります。そのとき上記二つの式はどうなるかみてみましょう。

h(x)のモデルから出力が正解に近ければ、lossの値が小さくなり、不正解なら大きくなります。

ロジスティック回帰でも、勾配降下法は、このlossが小さくなるようなwとbを探してくれます。

loss(損失関数)の選定は機械学習のモデルに合わせればよい

上記のようなlossの式を考えるのは難しいですね。

でも心配する必要はありません。

機械学習のモデルによって使うものが決まっているので、自分で考えることはありません。

使いたい機械学習モデルごとに決められたlossを使うようにしましょう。

ロジスティック回帰で0/1の分類をする

では、実際にscikit learnを使ってロジスティック回帰を使って、0/1の分類をしていきましょう。

scikit learnで線形回帰モデルを作ってみよう

scikit learnのインストール

まずは、scikit learnのインストールをします。

scikit learnは線形回帰などの機械学習を簡単に実行してくれるライブラリです。

Anacondaなどpythonの使える環境のTerminalやコマンドプロンプトで下記を実行します。

pip install scikit-learn

1	pip install scikit-learn

今回はirisというアヤメの品種データを使います。

ライブラリの読み込み

ライブラリにはデータを扱うpandas, numpy。

グラフを表示するmatplotlib, seaborn。

機械学習のscikitlearnを使います。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import train_test_split

scikitlearnからはロジスティック回帰のLogisticRegressionとデータを学習用と評価用に分けるtrain_test_splitを読み込んでいます。

データの準備と確認

データはseabornのライブラリに入っているのでそれを使います。

データを読み込んでデータを確認しましょう。

アヤメの品種はこのデータには３種[‘setosa’ ‘versicolor’ ‘virginica’]含まれていますが、２種[‘setosa’ ‘virginica’]に絞ります。

df = sns.load_dataset('iris')
# 品種の確認
print(df['species'].unique())
# 品種を2種類に絞る
df = df[(df['species']=='setosa') | (df['species']=='virginica')]
# データの一部確認
df.head()

df = sns.load_dataset('iris')

# 品種の確認

print(df['species'].unique())

# 品種を2種類に絞る

df = df[(df['species']=='setosa') | (df['species']=='virginica')]

# データの一部確認

df.head()

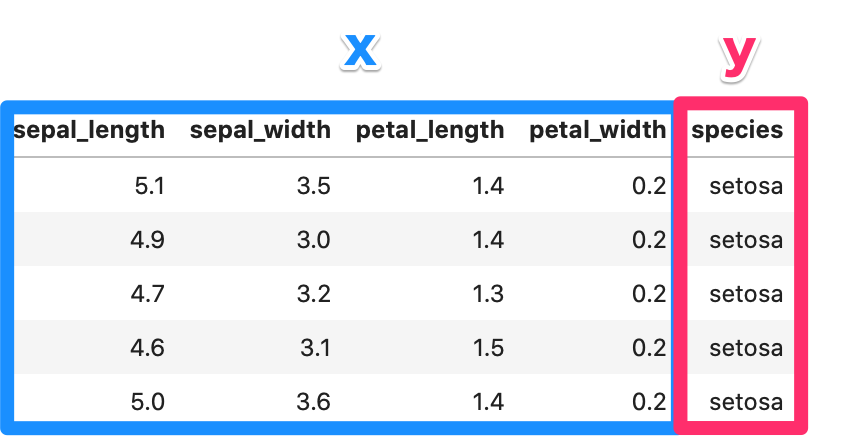
データには特徴量(説明変数)が4つあります。

それぞれ、花びらの大きさのデータです。

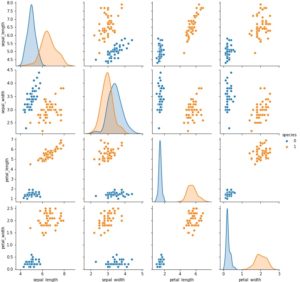
後は、散布図でデータを確認してみましょう。

sns.pairplot(df, hue='species')

1	sns.pairplot(df, hue='species')

品種でプロットが分かれているので、精度よく学習ができそうです。

yにあたるspecies列が文字列なので、0と1に置き換えて、xとyの値を取得します。

# setosa=0 virginica=1に変更
df['species'] = df['species'].map({'setosa': 0, 'virginica': 1})

# 説明変数と目的変数を分ける
x = df[['sepal_width', 'sepal_length', 'petal_width', 'petal_length']].values
y = df['species'].values

# データの行列数確認
print(x.shape)
print(y.shape)

# setosa=0 virginica=1に変更

df['species'] = df['species'].map({'setosa': 0, 'virginica': 1})

# 説明変数と目的変数を分ける

x = df[['sepal_width', 'sepal_length', 'petal_width', 'petal_length']].values

y = df['species'].values

# データの行列数確認

print(x.shape)

print(y.shape)

(100, 4)
(100,)

1 2	(100, 4) (100,)

100個分のデータがありますね。

機械学習では学習した結果がうまく行ったかどうか確認するために、学習用とテスト用でデータを分けます。

scikitlearnにはデータを分けるようの関数も用意されているので使ってみましょう。

# 学習用と評価用に分けます
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.1)

print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)

# 学習用と評価用に分けます

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.1)

print(x_train.shape)

print(x_test.shape)

print(y_train.shape)

print(y_test.shape)

train_test_splitではtest_sizeで分割する割合を指定できます。

今回は0.1なので1割をテスト用のデータにしています。

100個のデータが90:10に分けられていますね。

(90, 4)
(10, 4)
(90,)
(10,)

(90, 4)

(10, 4)

(90,)

(10,)

学習

データの準備ができたので、学習をしてみましょう。

# ロジスティック回帰の呼び出し
lr = LogisticRegression()
# 学習の実行
lr.fit(x_train, y_train)

# ロジスティック回帰の呼び出し

lr = LogisticRegression()

# 学習の実行

lr.fit(x_train, y_train)

結果確認

学習が完了したら、テスト用に分けたデータで精度の確認をしてみましょう。

まず、テストデータで機械学習の予測結果を受け取ります。

# テストデータで予測
y_pred = lr.predict(x_test)

1 2	# テストデータで予測 y_pred = lr.predict(x_test)

後は、この結果と教師データの答えとを照らし合わせて、精度を確認しましょう。

# 正解と一致数をカウント
correct_num = sum(y_pred == y_test)
# データの数
data_len = len(y_test)
#正解率の表示
print(f"正解率:{correct_num/data_len*100}%")

# 正解と一致数をカウント

correct_num = sum(y_pred == y_test)

# データの数

data_len = len(y_test)

#正解率の表示

print(f"正解率:{correct_num/data_len*100}%")

正解率:100.0%

1	正解率:100.0%

うまく学習ができ、精度の良い結果となりました。

時間があれば、他の品種の組み合わせでも試してみてください。

まとめ

この記事では、pythonのロジスティック回帰の分類モデルについて説明しました。

シグモイド関数など普段見慣れない複雑な数式も出てきましたが、繰り返し確認して理解を深めましょう。

基礎的な線形回帰の知識もこれを機に確認しておきましょう。

【CNN】職人がパチンコで理解する畳み込みニューラルネットワーク【機械学習】

DeepLearningのライブラリ　pytorchを使ってみよう