【scikit learn】線形回帰モデルを作ってみよう

Itoi Yoshihiko

横浜国立大学理工学部建築都市環境系学科卒
一級鉄筋技能士

機械学習を最初に学ぶときは線形回帰から始めていきます。

中学で習う下記のような１次式を復習することで、機械学習の基礎的な考えがわかります。

難しい数学の知識はできるだけ省いてできるだけ簡単に説明します。

ただ、中盤以降はpythonの基礎的な知識は必要ですので、関連記事等で確認しつつ読み進めてください。

線形回帰とは？

機械学習の入門では、線形回帰の理解は必須になります。

ここでは、値を予測をするAIを開発するケースを想定し、線形回帰をどう活用するのか見ていきましょう。

画像の物体検知AIなども、ここでの知識がベースになります。

家の価格を予測する事例で線形回帰を理解しよう

今回は、家の価格を予測する事例を考えます。

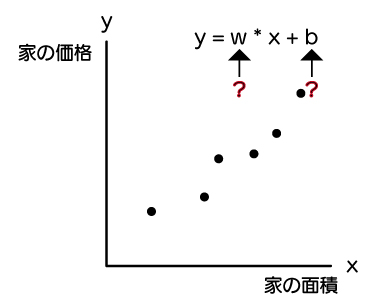
冒頭でも出しましたが、「家の面積」と「家の価格」のデータをプロットしたものと想定します。

まだ、価格がわからない家があったとしましょう。

今から、その家を購入したいと思ったとき、できるだけお得に購入したいですね。

お得かどうかは、参考にできる価格があると良いでしょう。

そのために家の価格を予測する必要があります。

機械学習は近似式を算出する

こういうとき、機械学習はどのようなことを行なってくれるのでしょうか？

手元には下記のように、6つプロットされたx:家の面積とy:家の価格のデータがありますが、このままでは、wとbがわからないので、近似式がわかりません。

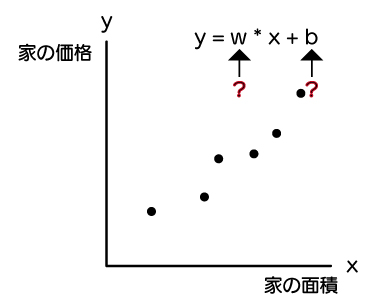
近似式がわからないと、予測したい家の面積が分かったとしても、家の価格が求められません。

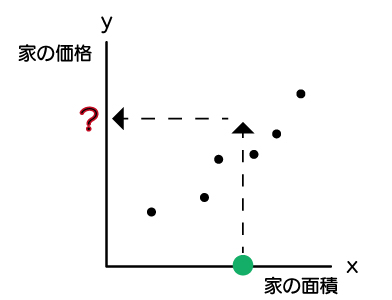
機械学習では、このwとbを求めてくれます。

近似式y = w * x + b　各項の説明

中学校では、y = a * x + bでしたが、ここでは、y = w * x + bでしたね。

それぞれ、呼び方があります。

y: 目的変数
x: 説明変数 / 特徴量
w: 重み
b: バイアス
w, b: パラメータ

xは特徴量という方が多いと思います。

近似式の特徴量xが1つの場合を単回帰、複数ある場合は重回帰という

xの特徴量が1つの場合を単回帰といいますが、複数ある場合は重回帰といいます。

家の価格が面積だけで正確に求まるわけないよと思った方は、この重回帰を使うことになります。

例えば、家の面積だけでなく、部屋数、リビングの面積などです。

重回帰は下記のように表されます。

$$ y = b + w_1x_1 + … + w_mx_m $$

単回帰から、特徴量xがm個に増えたものです。

$x^2$を増やすと2次式ですが、特徴量が増えたと考えても良いでしょう。

$b$は$w_0$とする場合もあります。

近似式のwやbの最適な値を求めるには勾配降下法を使う

機械が決めてくれるwやbの最適な値とはなんでしょう？

どうやって決めれば良いのでしょうか？

それは、以下のように「今あるデータ」と「1次式」の差が一番小さくなるところです。

今あるデータは教師データといい、1次式などはモデルともいいます。

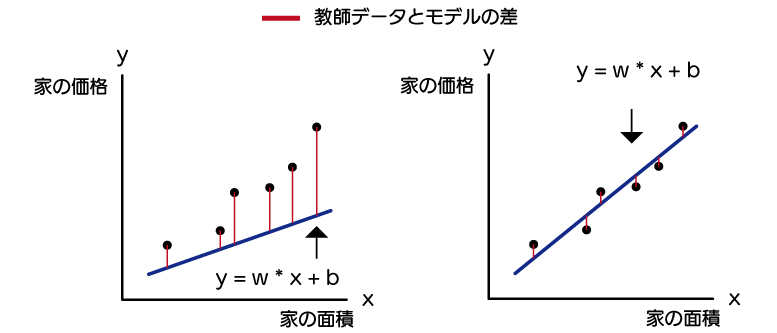
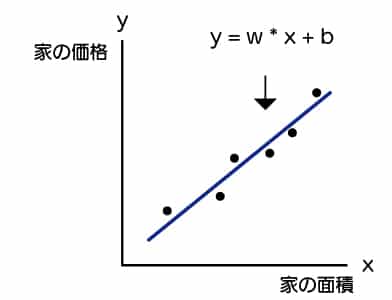
機械には左より、右のようになるwとbを求めて欲しいものです。

そのために、赤い線の教師データとモデルの差を最小になるwとbを機械に求めてもらう必要があります。

その方法に勾配降下法というものを使います。

勾配降下法では、教師データとモデルの差をlossとして定義して、lossが最小になるようなwとbを探します。

lossのことを損失関数とも呼びます。

今回であれば、lossには一般的に使われる、平均二乗誤差で考えると良いでしょう。

$$ loss = ((Y_1-\hat{Y_1})^2 + (Y_2-\hat{Y_2})^2 + (Y_3-\hat{Y_3})^2 + (Y_4-\hat{Y_4})^2 + (Y_5-\hat{Y_5})^2 + (Y_6-\hat{Y_6})^2)/6 $$

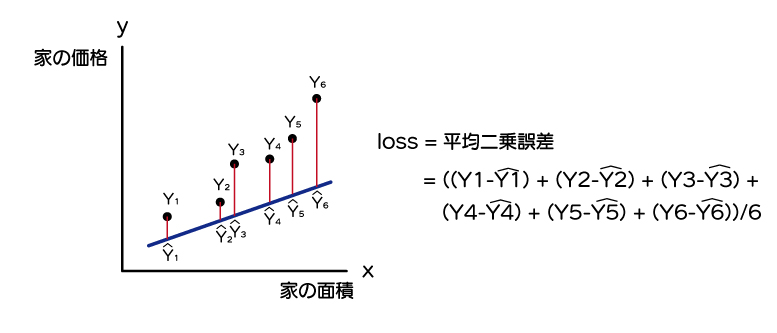
$ \hat{Y}$はワイハットと呼びます。1次式のモデルで算出されるYの値を指します。

このlossはwやbの値によって、大きなったり、小さくなったりしますね。

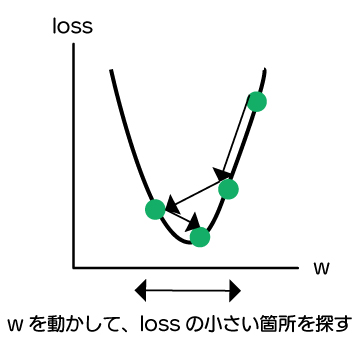
wの変化による、lossの変化を下記図で示します。

機械はこの小さくなるところを探します。この過程は機械が学習しているといって良いでしょう。

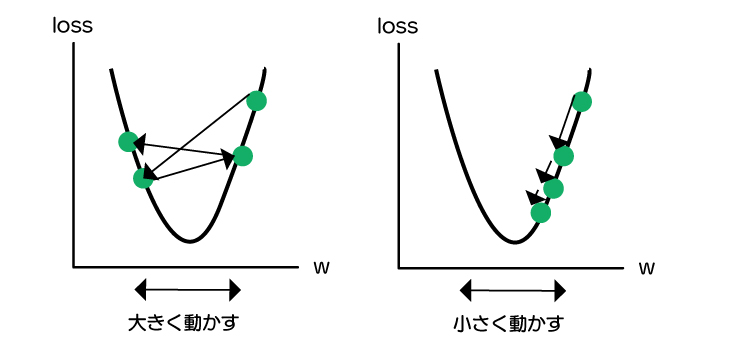
このとき、大きく動かすか、小さく動かすかで、lossが最小にならない場合もありますし、最小になるまで時間がかかる場合もあります。

この動かす量を学習率(learning rate)というもので調整します。

最適化アルゴリズムとはlossを最小にすること

今回は、勾配降下法というものを紹介しましたが、これを最適化アルゴリズム（optimizer）と言います。

他にも色々な種類がありますが、必ず学習率は調整するので覚えておく必要があります。

次に紹介するscikit learnでは、実はこの知識がなくても使うことができますが、この線形回帰の段階でなんとなく理解しておかないと画像AIとかでは何をしているのかわからなくなってしまいますので、覚えておくと良いでしょう。

モデルとアルゴリズム

機械学習における「モデル」とは数式のことです。単回帰の例でいえば、近似式y = w * x + bがモデルになります。
この「モデル」のwやbのパラメータをどういった考え方に基づいて計算するのか？を示すのが「アルゴリズム」になります。
別の言い方をすれば、「アルゴリズム」とは、どうやって最適な近似式を算出するのか？といった考え方のことを指します。

データ→何らかのアルゴリズム→モデル

例：単回帰
家の面積/部屋数/リビングの面積→最小二乗法、勾配降下法(アルゴリズム)→y = w * x + b

scikit learnとは？

scikit learnは線形回帰などの機械学習を簡単に実行してくれるライブラリです。

scikit learnのインストール

Anacondaなどpythonの使える環境のTerminalやコマンドプロンプトで下記を実行します。

pip install scikit-learn

1	pip install scikit-learn

scikit learnで線形回帰モデルを作ってみよう

では、実際にscikit learnを使って線形回帰モデルを作ってみましょう。

ライブラリをインポート

ライブラリには、グラフも表示したいのでmatplotlibと数値演算用のnumpyをインポートします。

from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression

import matplotlib.pyplot as plt

import numpy as np

データを用意する

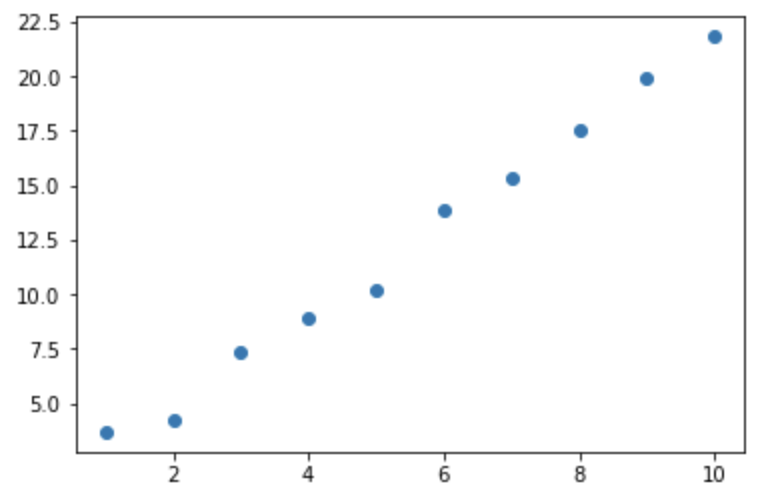
次にデータを用意しますが、分かりやすさのため、w=2、b=1の乱数を混ぜたデータを10点用意してそのデータで動かしていきましょう。

データは下記コードで用意します。

データを作っているところは慣れている方は「pythonに慣れている方はこちらでもOK」のところを使ってください。

# 1次式のwとb
w = 2
b = 1

# データ作成
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = []
for x_data in x:
    rand = np.random.randint(-10, 10)/10
    y.append(b + w * x_data + rand)
    
# pythonに慣れている方はこちらでもOK
x = range(1,11)
y = [b + w * x_data + np.random.randint(-10, 10)/10 for x_data in x]

# データを整形
x = np.array(x).reshape([10,1])
y = np.array(y)

# グラフ表示    
plt.scatter(x, y)

# 1次式のwとb

w = 2

b = 1

# データ作成

x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

y = []

for x_data in x:

rand = np.random.randint(-10, 10)/10

y.append(b + w * x_data + rand)

# pythonに慣れている方はこちらでもOK

x = range(1,11)

y = [b + w * x_data + np.random.randint(-10, 10)/10 for x_data in x]

# データを整形

x = np.array(x).reshape([10,1])

y = np.array(y)

# グラフ表示

plt.scatter(x, y)

データを途中整形していますが、機械学習ではよく下記のような表データで読み込みます。

その場合、xは（n行, m列）、yはn個のデータで使います。

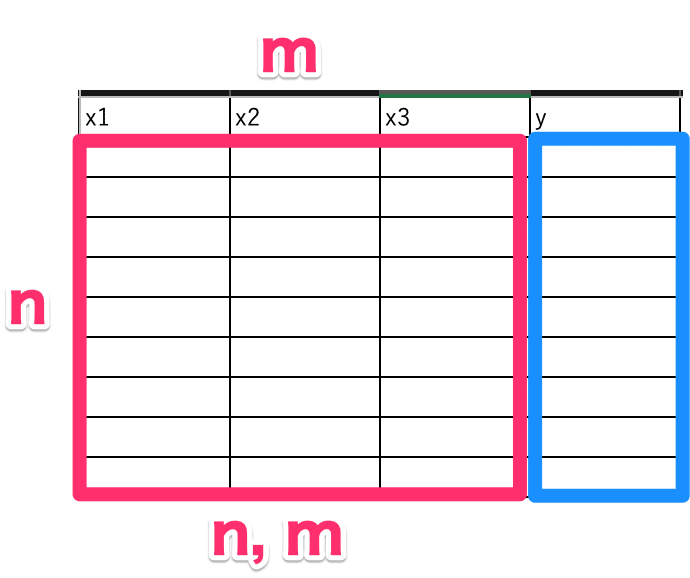
ですので、今回はxをn=10、m=1のデータにしたいので、reshapeメソッドで[10行,1列]にしています。

学習

学習は、簡単でLinearRegressionを呼び出して、fitメソッドに、xとyを入れるだけです。

学習というと大袈裟かもしれませんが、lossの最小化をします。

特に何も指定することなく、fitを使うだけで後はメソッド内でしてくれます。

# 線形回帰
lr = LinearRegression()
# 学習 fit関数を使うだけ
lr.fit(x, y)

# 線形回帰

lr = LinearRegression()

# 学習 fit関数を使うだけ

lr.fit(x, y)

確認

学習後のwとbを確認してみましょう。

coef_とintercept_で確認ができます。

print("w = ", lr.coef_)
print("b =", lr.intercept_)

1 2	print("w = ", lr.coef_) print("b =", lr.intercept_)

w =  [2.09818182]
b = 0.7400000000000002

1 2	w = [2.09818182] b = 0.7400000000000002

乱数を入れていたので、少し値は違いますが、おおよそw = 2 、 b = 1に近い数字になっています。

＊データは乱数を混ぜているので、結果は実行毎に違います。大体w=2、b=1になっていればOKです。

新しいデータで予測

手元にあるデータで学習が終わったので、教師データにはないデータで、予測をしてみましょう。

今回は、適当に5.5と10.3を使います。

x_test = np.array([5.5, 10.3]).reshape(2,1)
lr.predict(x_test)

1 2	x_test = np.array([5.5, 10.3]).reshape(2,1) lr.predict(x_test)

array([12.28      , 22.35127273])

1	array([12.28 , 22.35127273])

大体合ってそうですね。

＊データは乱数を混ぜているので、結果は実行毎に違います。

これで、線形回帰で学習させ、新しいデータを予測することができました。

まとめ

scikit learnで線形回帰モデルを作ってみました。

「回帰」のように少しとっつきにくい数学的な用語や、「アルゴリズム」や「モデル」、「ライブラリ」といった機械学習の用語も理解することが大切です。

線形回帰はモデルが直感的に分かりやすいので、何度も復習して使いこなしましょう。