横浜国立大学理工学部建築都市環境系学科卒
一級鉄筋技能士
唎酒師
狂人のごとく特定の分野、中小企業を理解し、国の補助金を獲得します。最近は中小企業のM&Aにも挑戦中
型枠が崩壊しないかどうかのポイントは、型枠にかかる荷重と支保工材の数やピッチです。
なんとなく型枠材料が多ければ、大きな荷重であっても耐えられるような気がしますね。
この記事では、詳細な型枠の設計方法について見ていきましょう。
目次
型枠支保工の設計の3ステップ
型枠支保工の設計は、以下の3ステップになります。
①設計荷重の算定
②単純モデル化
③応力・変位の照査
1.設計荷重の算定
まずは、鉛直方向の荷重を算定しましょう。
鉛直方向の荷重には、死荷重(型枠・支保工,コンクリート,鉄筋,作業員,施工機械等)や作業荷重があります。
死荷重
|
1 2 3 4 5 6 |
無筋コンクリートの単位体積重量 γ1=23.0(kN/m3) 鉄筋コンクリートの単位体積重量 γ2=23.0(kN/m3) 型枠の単位体積重量 γ3=0.5(kN/m3) |
作業荷重
|
1 2 3 4 |
労働安全衛生規則に則る場合の等分布荷重 p1=1.5(kN/m3) コンクリート標準示方書に則る場合の等分布荷重 p2=2.5(kN/m3) |
次に、水平方向の荷重を算定しましょう。
地震,振動,衝撃等の荷重,型枠の傾斜等による水平方向の荷重を設定します。
一般には、設計鉛直荷重の 5%、 工場製作精度で組立てる場合は鉛直荷重の 2.5%に相当する水平荷重を支保工頂部に作用させます。
実際に、水平荷重が作用しない場合であっても、水平力に対する型枠支保工全体の安定性を考慮するために、水平方向の荷重を設定します。
この荷重を照査水平方向荷重といいます。
|
1 2 |
照査水平方向荷重 p=1.5(kN/m3) |
コンクリートの側圧の算定
使用材料,打込み速度,コンクリート温度等の条件によりコンクリートの側圧を設定します。
コンクリート側圧は型枠の設計において最も支配的となる荷重となります。
コンクリートの側圧に影響する要因は、以下の通りです。
①構造物条件 :部材の断面寸法(柱、壁)
②コンクリートの条件 :材料、配合、スランプ、凝結時間、コンクリート温度
③施工条件 :打上がり速度、締固め方法、再振動の有無
以上の要因に加えて、コンクリートの流動性(スランプ)に応じて側圧式を適切に選択する必要があります。
①高流動コンクリートの場合
|
1 2 3 4 |
Pw=Wc*H Pw:液圧(kN/m2) Wc:コンクリート単位体積重量(=23.5kN/m3) H:コンクリート打ち込み高さ(m) |
②スランプが10cm程度の場合
|
1 2 3 4 5 6 7 8 9 10 |
#柱の場合 P=Wc/3*[1+(100R/(T+20))] #壁の場合 P=Wc/3*[1+(150+30R)/(T+20))] P:側圧(kN/m2) Wc:コンクリート単位重量(kN/m3) R:打設速度(m/h) T:打ち込み時のコンクリート温度(℃) |
以上の式に見られるように、コンクリートの側圧は、コンクリートの打ち込み高さ、打ち込み速度、コンクリート温度に影響を大きく受けます。
打設速度は2-3m/hが一般的
コンクリート温度は25-30度前後
側圧が大きくなると型枠「浮く」現象が発生し、崩壊する可能性がでてくる
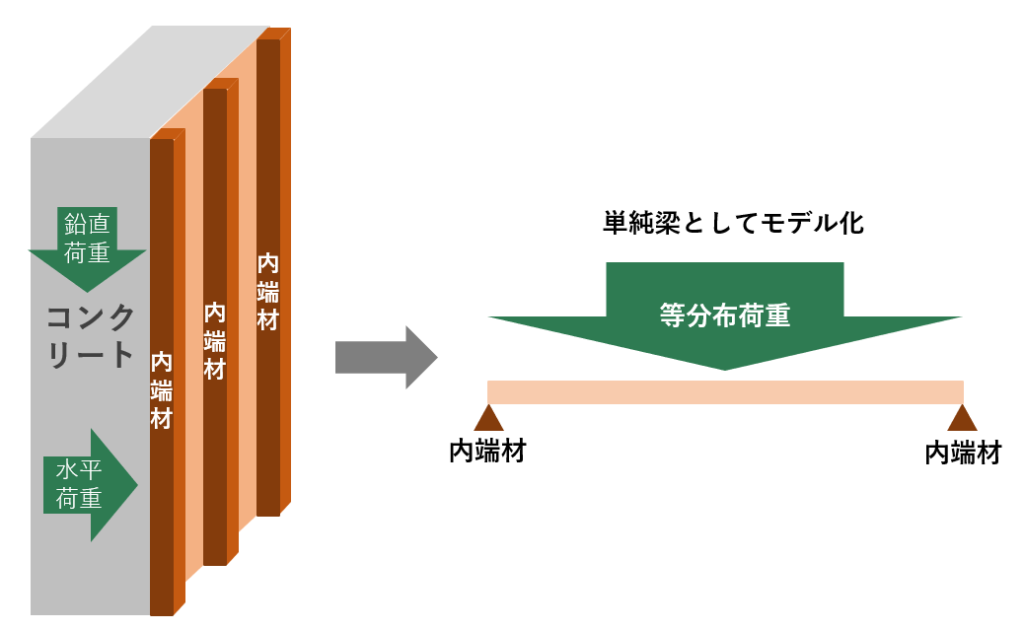
2.単純モデル化
荷重を設定した後、構造を理解したうえで可能な限り単純化したモデル(単純梁)を作成します。
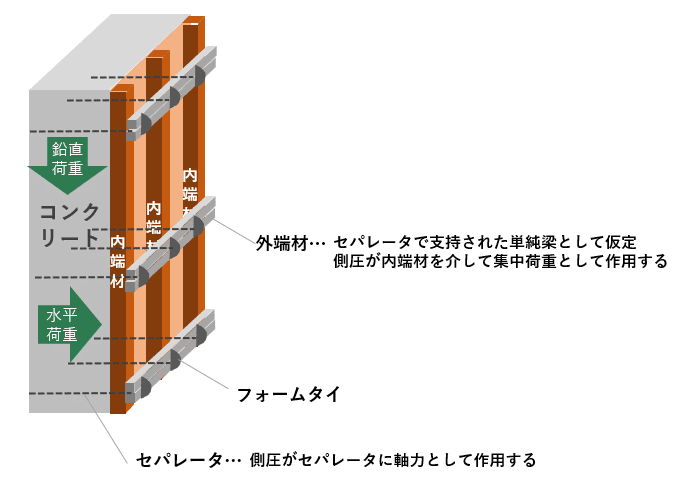
内端材は外端材で支持された単純梁として考えます。
同様に、外端材はセパレータで支持された単純梁として考えます。
このように、型枠に発生する応力や使用材料をできるだけ単純化させたモデルを用いることで、部材が応力に対応できるのかどうかを照査していきます。
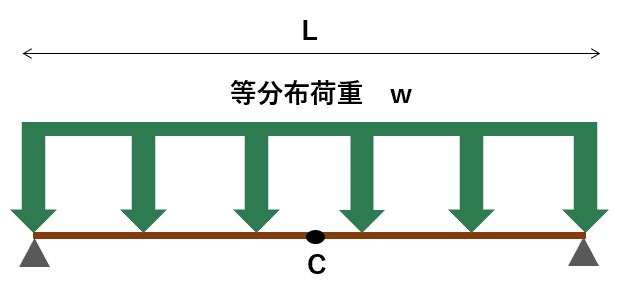
3.応力・変位の照査
発生断面力や発生変位が各部材の材料の応力や変位の許容値以内になるかどうかを照査します。
|
1 2 3 4 5 6 7 |
#最大曲げモーメントMc Mc=w*L^2/8 #最大たわみδ δ=5*w*L^4/384*E*I E:ヤング係数 I:断面二次モーメント |
以上のように算出した最大曲げモーメントと最大たわみ量に対して、使用する材料の許容応力度と許容たわみ量を比較することで使用材料の検討を行います。
使用する材料の許容応力度と許容たわみ量と比較する
まずは、許容応力度について見ていきましょう。
合板の許容応力度比較
型枠の合板に関しては、許容応力度は16.5(N/mm2)とわかります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#応力単位荷重 w0=28.6(kN/m^2) #荷重分担幅 @=0.9(m) #梁材長さ L=0.3(m) #部材厚さ t=12(mm) #断面係数 Z=21600(mm^3) #断面二次モーメント I=@*t^3/12(mm^4) =1296000(mm^4) #ヤング係数 5.5*10^3(N/mm^2) #合板に作用する荷重 w=w0*@=28.6*0.9=25.7(kN/m) #最大曲げモーメント M=w*L^2/8 =0.289(kN/m) #許容曲げ応力度 σ=M/Z=289000/21600 =13.37(n/mm^2) <16.5(N/mm^2)→OK!! |
合板の許容たわみ量比較
型枠の許容たわみ量は、通常 3mm、外観が目立つ部分では 2mm 以内とします。
|
1 |
δ=(たわみ量)/(支保工スパン長)<1/240 |
同様な条件でたわみ量を計算してみます。
|
1 2 3 4 |
δ=5*w*L^4/384*E*I =5*25.7*300^4/384*5.5*10^3*1296000 =0.38(mm) <3(mm)→OK!! |
まとめ
煩雑な計算式が出てきましたが、型枠がどのように設計されているのかイメージできたでしょうか。
単純梁としてモデル化した場合、単純梁のスパン長さが小さいほど断面力は小さくなります。
使用材料の許容応力度や許容たわみ量は決定値なので、しっかり計算ができれば比較検討は簡単です。
設計の3ステップをしっかり理解しておきましょう。