
横浜国立大学理工学部建築都市環境系学科卒
一級鉄筋技能士
唎酒師
狂人のごとく特定の分野、中小企業を理解し、国の補助金を獲得します。最近は中小企業のM&Aにも挑戦中
機械学習は精度を確認することが必須になります。
精度評価をしないで使い始めると、学習時と違って精度が全然出ないということになりかねません。
精度評価について理解していきましょう。
目次
精度評価について
機械学習はどれくらいの精度になったかが大事になります。
機械学習の判定は、判定根拠が人間からすると複雑すぎて理解ができないため、精度というわかりやすいもので判断していくためです。
機械学習では精度が一番大切
例えば、従来の画像処理の検査で考えてみましょう。
ある製品の良品を不良品を判定したいとします。
従来の画像処理では、色々な画像処理を組み合わせることで、傷や汚れなど異常箇所を検知して判定します。
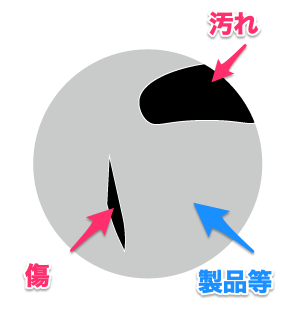
この処理を組み合わせて、このように不良と判断していますと説明できます。
しかし、機械学習においてはこの画像は良品、この画像は不良品といったように、良品/不良品などの情報を渡すだけです。
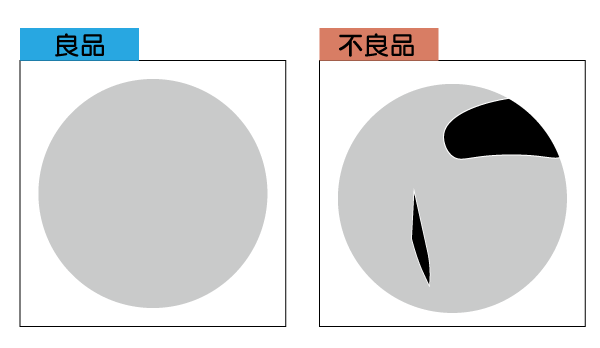
ここに傷があるから汚れがあるなどは教えません。
なので、どのようにして不良品と判定したか不明で説明ができません。
そこで必要になるのが、精度です。
「機械学習がどういった処理をしたかわからないけど、〇〇%の精度で判定してくれるから使える!」ということを確認します。
精度評価とはデータを学習、バリデーション、テスト用に分割すること
精度評価ですることは非常に簡単で、持っているデータを分割するだけです。
機械学習は大量のデータを必要とします。
データ量が多いと精度が上がるためです。
そのデータは全て学習に使わず、1.学習、2.バリデーション、3.テスト用の3つに分けます。
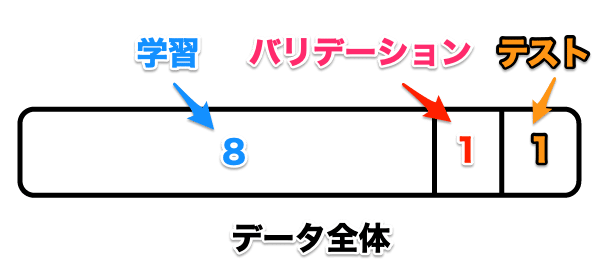
これは好みにもよりますが、8:1:1=学習:バリデーション:テスト用の割合で分けると良いでしょう。
| 学習 | 学習で使うデータ |
| バリデーション | 学習のハイパーパラメータ(学習率など)を調整して、一番精度の良いパラメータを確認するデータ |
| テスト | 学習後最終的に精度確認用のデータ |
バリデーションは「検証」を意味します。
バリデーションは、学習率やディープラーニングの層の数などハイパーパラメータを調整するときに、一番精度が出るパラメータを探すために使うデータになります。
ハイパーパラメータは機械学習で人が調整が必要なパラメータ全般を指します。
学習:テスト=8:2くらいに分けて、テスト用のデータでハイパーパラメータを調整しても、問題ありません。
データ数が膨大な場合は調整が必要
データが数万と膨大にある場合は、8:1:1とせずにテスト用データは1000にするなど、精度を確認するのに十分なデータ量で設定すると良いでしょう。
どれくらいの量か?というのは特に決まっているわけではないので、持っているデータからご自身の経験則で判断してください。
例えば、10万のデータがあり良品/不良品の2項分類では、テスト用のデータは1000もあれば十分でしょう。
しかし、何種類も分類する多項分類で1000種類を分類する場合1000では足りず、最低1万程度のデータを用意しましょう。
このように、比率は目安であり、精度を確認するのに十分なテストデータを用意することが大切です。
精度評価とはデータを学習、バリデーション、テスト用に分けること
8:1:1=学習:バリデーション:テストといった感じでデータを分割する
データ量に応じて分割する割合や量を調整する
なぜデータの分割が必要なの?
データを分けて、それぞれのデータで精度を確認するのは、オーバーフィッティング、アンダーフィッティングという状態を確認するためです。
具体的に説明していきます。
オーバーフィッティング(過学習)、アンダーフィッティング(過小学習)を防ぐ
これらがどのような状態かというのを説明していきます。
次のような、線型回帰で考えていきます。
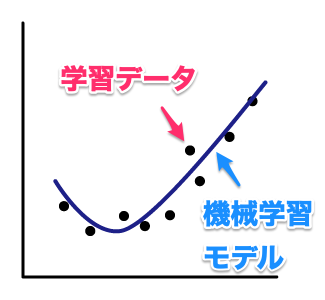
機械学習において一番良いのは、今まで集めた学習データにフィットしすぎず、今後の予測や判定したいデータでも精度が出る状態です。
学習、テストデータの精度を確認することで、ジャストフィットになるようにする必要があります。
| アンダーフィッティング | ジャストフィット | オーバーフィッティング | |
|---|---|---|---|
| イメージ | 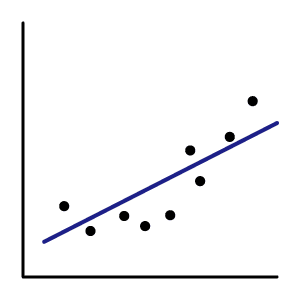 学習がうまく行っていない状態 |
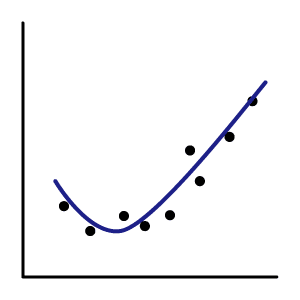 学習がうまくいき、運用に使える状態 |
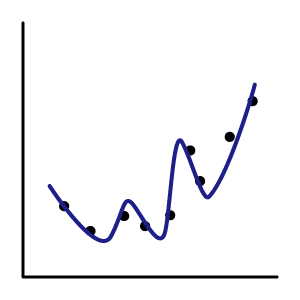 学習はうまく行っているが、学習データにフィットしすぎて、運用時には精度が十分に出ない状態。 |
| 精度や 決定係数等 |
学習とテストデータの精度が70,80%と低い ex:学習(70.5%)、テスト(68.0%) |
学習とテストデータの精度が90%以上と高くその差0.*%程度 ex:学習(95.6%)、テスト(95.0%) |
学習データの精度が高いが、テストデータとの精度に差がある ex:学習(96.8%)、テスト(90.0%) |
| 対策 | 機械学習モデルの変更。 ハイパーパラメータを調整。 データを増やす。 |
特にないが、必要とする精度によって 機械学習のモデルを見直したり、 データを増やす。 |
特徴量が多い場合、データを増やす。 正則化項を使う。 CNNならドロップアウト層等の調整。 よりシンプルなモデルに変更。 |
機械学習は学習によって自動で判別や予測する方法を取得してくれますが、このように人が調整しなければならないところもあります。
精度評価の方法
精度の評価は、機械学習で何をするかによって内容が変わります。
値予測には標準誤差RMSEと決定係数R2を使う
まず、値の予測です。
正解値を\(y\)、予測値\(\hat{y}\)とします。
標準誤差RMSEは値が小さいほど良い
二乗平均平方根誤差(RMSE:Root Mean Squared Error)は次の式で表されます。
$$決定係数 = \sqrt{\frac{1}{n}\sum_{i=1}^{n-1} (y_i-\hat{y}_i)^2}$$
\(y\):正解値
\(\hat{y}\):予測値
\(n\):サンプル数
予測値との差を二乗平均して、ルートで戻しています。
予測値との差を見ているので値が小さい方が精度が高くなります。
pythonでは、scikit-learnを使うことで、簡単に算出することができます。
|
1 2 3 4 |
from sklearn.metrics import mean_absolute_error y = [1.0, 2.0, 3.0, 4.0, 5.0] y_pred = [1.1, 1.9, 3.3, 4.1, 5.0] print(mean_absolute_error(y, y_pred)) |
|
1 |
0.11999999999999993 |
決定係数R2は1に近いほど良い
決定係数は次の式で表されます。
$$RMSE = 1-\frac{\sum_{i=1}^{n-1} (y_i-\hat{y}_i)^2}{\sum_{i=1}^{n-1} (y_i-\bar{y}_i)^2}$$
\(y\):正解値
\(\hat{y}\):予測値
\(\bar{y}\):平均値
\(n\):サンプル数
値は0〜1となり、1に近いほど、うまく予測できていることになります。
こちらも同様に、sikit-learnの関数を使うと簡単に算出できます。
|
1 2 3 4 |
from sklearn.metrics import r2_score y = [1.0, 2.0, 3.0, 4.0, 5.0] y_pred = [1.1, 1.9, 3.3, 4.1, 5.0] print(r2_score(y, y_pred)) |
|
1 |
0.988 |
分類
分類では0か1か予測できたかの正解率を見ますが、いくつか指標があります。
各指標
0は0と予測できればいいですが、0を1を予測するときもあります。
これを以下のような表にすることができます。
| 1(真) | 0(偽) | |
|---|---|---|
| 機械の予測 1(真) | TP (True Positive) | FP (False Positive) |
| 機械の予測 0(偽) | FN (False Negative) | TN (True Negative) |
例えば、10個のサンプル(真偽5ずつ)が下記のような結果だったとします。
| 1(真) | 0(偽) | |
|---|---|---|
| 機械の予測 1(真) | 4 | 2 |
| 機械の予測 0(偽) | 1 | 3 |
python算出するにはこちらも、scikit-learnのライブラリを活用します。
|
1 2 3 4 5 6 7 8 9 |
from sklearn.metrics import confusion_matrix y = [0,0,0,0,0,1,1,1,1,1] y_pred = [0,0,1,1,0,1,0,1,1,1] c_mat = confusion_matrix(y, y_pred) TN = c_mat[0][0] FP = c_mat[0][1] FN = c_mat[1][0] TP = c_mat[1][1] print(f"TP:{TP} FP:{FP} TN:{TN} FN:{FN}") |
|
1 |
TP:4 FP:1 TN:3 FN:2 |
このTP,TN,FP,FNを使った次のような指標があります。
| 指標 | 式 | 意味 | 計算例 |
|---|---|---|---|
| 正解率(Accuracy) | \(\frac{TP+TN}{TP+FP+TN+FN}\) | 0と1の正解した比率 | \(0.70=\frac{4+3}{4+1+3+2}\) |
| 適合率(Precision) | \(\frac{TP}{TP+FP}\) | 1と予測した内、実際に1の比率 | \(0.67=\frac{4}{4+2}\) |
| 再現率(Recall) | \(\frac{TP}{TP+FN}\) | 実際の1の内、1と正解した比率 | \(0.80=\frac{4}{4+1}\) |
| 特異率(Specificity) | \(\frac{TN}{TN+FP}\) | 実際の0の内、0と正解した比率 | \(0.60=\frac{3}{3+2}\) |
| F値(F1 Score) | \(\frac{2*Recall*Precision}{Recall+Precision}\) | PrecisionとRecallの調和平均 | \(0.73=\frac{2*0.80*0.67}{0.80+0.67}\) |
とりあえず、F値を使っておけばバランスの取れた精度評価ができます。
各指標をそのまま算出することもできます。
|
1 2 3 4 5 |
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score print(f"accuracy: {accuracy_score(y, y_pred)}") print(f"precision: {precision_score(y, y_pred)}") print(f"recall: {recall_score(y, y_pred)}") print(f"f1 score: {f1_score(y, y_pred)}") |
|
1 2 3 4 |
accuracy: 0.7 precision: 0.6666666666666666 recall: 0.8 f1 score: 0.7272727272727272 |
まとめ
この記事では機械学習の精度評価について説明しました。
難しい数式がでてきましたが、ライブラリを活用することで簡単に算出できます。
思い出したいときに見直しをする程度で押さえておきましょう。


